ما هو تحويل الميزات الثابتة القياس (SIFT)؟

في هذه الأيام، تأتي العديد من الأجهزة الذكية التي نستخدمها، من الهواتف والكاميرات إلى أنظمة المنزل الذكي، مزودة بحلول الذكاء الاصطناعي التي يمكنها التعرف على الوجوه والأشياء وحتى المشاهد المرئية بأكملها. تأتي هذه القدرة من رؤية الكمبيوتر، وهو مجال من مجالات الذكاء الاصطناعي يمكّن الآلات من فهم وتفسير الصور ومقاطع الفيديو.

على سبيل المثال، إذا التقطت صورة لبرج إيفل من أي زاوية أو مسافة، فسيظل بإمكان جهازك التعرف عليها عادةً باستخدام رؤية الكمبيوتر وتنظيمها في المجلد الصحيح في معرض الصور الخاص بك. على الرغم من أن هذا يبدو واضحًا ومباشرًا، إلا أن التعرف على الكائنات ليس دائمًا بالأمر البسيط. يمكن أن تبدو الصور مختلفة جدًا اعتمادًا على حجمها أو زاويتها أو مقياسها أو إضاءتها، مما يجعل من الصعب على الآلات تحديدها باستمرار. 

للمساعدة في حل هذه المشكلة، طوّر الباحثون خوارزمية للرؤية الحاسوبية تُعرف باسم "تحويل الميزات الثابتة بالمقياس" أو SIFT. تتيح هذه الخوارزمية إمكانية detect الأجسام في ظروف مشاهدة مختلفة. صُممت خوارزمية SIFT، التي ابتكرها ديفيد لوي في عام 1999، للعثور على النقاط الرئيسية الفريدة في الصورة ووصفها، مثل الزوايا أو الحواف أو الأنماط التي تظل قابلة للتمييز حتى عند تغيير حجم الصورة أو تدويرها أو إضاءتها بشكل مختلف.

قبل نماذج الرؤية الحاسوبية القائمة على التعلم العميق مثل Ultralytics YOLO11 كانت تقنية SIFT تقنية مستخدمة على نطاق واسع في الرؤية الحاسوبية. كان نهجًا قياسيًا لمهام مثل التعرف على الأشياء، حيث يكون الهدف هو تحديد عنصر معين في الصورة، ومطابقة الصور، حيث تتم محاذاة الصور من خلال إيجاد ميزات الصور المتداخلة.

في هذه المقالة، سوف نستكشف SIFT مع نظرة عامة سريعة على ماهيته، وكيف يعمل على مستوى عالٍ، ولماذا هو مهم في تطور الرؤية الحاسوبية. هيا بنا نبدأ!

لماذا تعتبر خوارزمية SIFT ضرورية للرؤية الحاسوبية؟

في الصورة، يمكن أن يظهر الكائن بعدة طرق مختلفة. على سبيل المثال، قد يتم تصوير كوب القهوة من الأعلى أو من الجانب أو في ضوء الشمس الساطع أو تحت مصباح دافئ. يمكن أن يبدو الكوب نفسه أكبر أيضًا عندما يكون قريبًا من الكاميرا وأصغر عندما يكون أبعد.

كل هذه الاختلافات تجعل تعليم الكمبيوتر التعرف على كائن مهمة معقدة. تتطلب مهمة الرؤية الحاسوبية هذه، والمعروفة باسم اكتشاف الكائنات، أن تحدد نماذج Vision AI الكائنات وتحدد موقعها بدقة، حتى عندما يتغير حجمها أو زاويتها أو ظروف الإضاءة.

لجعل هذا ممكنًا، تعتمد رؤية الكمبيوتر على عملية تسمى استخراج الميزات أو الكشف عنها. بدلاً من محاولة فهم الصورة بأكملها مرة واحدة، يبحث النموذج عن ميزات صورة مميزة مثل الزوايا الحادة أو الأنماط أو الأنسجة الفريدة التي تظل قابلة للتمييز عبر الزوايا والمقاييس وظروف الإضاءة.

على وجه الخصوص، هذا ما تم تصميم Scale Invariant Feature Transform، أو SIFT، للقيام به. SIFT هي خوارزمية لاكتشاف الميزات ووصفها يمكنها تحديد الكائنات في الصور بشكل موثوق، بغض النظر عن كيفية التقاطها.

تحقيق ثبات المقياس

تتمتع خوارزمية SIFT ببعض الخصائص المهمة التي تجعلها مفيدة للتعرف على الكائنات. إحدى الخصائص الرئيسية تسمى الثبات القياسي (scale invariance). هذا يعني أن SIFT يمكنها التعرف على أجزاء مختلفة من الكائن، سواء كان يبدو كبيرًا وقريبًا من الكاميرا أو صغيرًا وبعيدًا. حتى إذا كان الكائن غير مرئي تمامًا، يمكن للخوارزمية التقاط نفس النقاط الرئيسية.

يفعل ذلك باستخدام مفهوم يسمى نظرية الفضاء القياسي. ببساطة، يتم تمويه الصورة بمستويات مختلفة لإنشاء إصدارات متعددة. ثم يبحث SIFT في هذه الإصدارات للعثور على الأنماط والتفاصيل التي تظل كما هي، بغض النظر عن كيفية تغير حجم الصورة أو حدتها. 

على سبيل المثال، ستبدو لافتة الطريق التي تم تصويرها من على بُعد بضعة أمتار أكبر بكثير من نفس اللافتة التي تم التقاطها من مسافة بعيدة، ولكن لا يزال بإمكان SIFT detect نفس السمات المميزة. هذا يجعل من الممكن مطابقة الصورتين بشكل صحيح، على الرغم من أن اللافتة تظهر بمقاييس مختلفة جداً.

ضمان ثبات الدوران

يمكن أن تظهر الكائنات في الصور أيضًا مستدارة، وأحيانًا رأسًا على عقب. تعالج SIFT هذا من خلال خاصية تسمى ثبات الدوران. لكل نقطة رئيسية تكتشفها، تحدد الخوارزمية اتجاهًا ثابتًا بناءً على تدرجات الصورة المحلية. بهذه الطريقة، يمكن التعرف على نفس الكائن بغض النظر عن كيفية تدويره.

يمكنك التفكير في الأمر على أنه وضع علامة على كل نقطة رئيسية بسهم صغير يوضح الاتجاه الذي تواجهه. من خلال محاذاة الميزات مع هذه الاتجاهات، يضمن SIFT تطابق النقاط الرئيسية بشكل صحيح حتى عند تدوير الكائن. على سبيل المثال، لا يزال من الممكن تحديد معلم بارز تم التقاطه في صورة منظر طبيعي بشكل صحيح حتى إذا تم التقاط صورة أخرى له مع إمالة الكاميرا بزاوية.

المرونة في مواجهة اختلافات الصور الأخرى

بالإضافة إلى الحجم والتدوير، يمكن أن تتغير الصور أيضًا بطرق أخرى، مثل تغييرات الإضاءة. قد ينتقل الضوء على الجسم من ساطع إلى خافت، وقد تتغير زاوية الكاميرا قليلاً، أو قد تكون الصورة ضبابية أو مشوشة.

تم تصميم SIFT للتعامل مع هذه الأنواع من الاختلافات. وهي تفعل ذلك من خلال التركيز على النقاط الرئيسية المميزة وعالية التباين، لأن هذه الميزات أقل تأثراً بالتغيرات في الإضاءة أو التحولات الصغيرة في وجهة النظر. ونتيجة لذلك، تميل SIFT إلى أن تكون أكثر موثوقية من طرق اكتشاف الحواف أو الزوايا البسيطة، والتي غالبًا ما تفشل عند تغير الظروف.

‍

ضع في اعتبارك لوحة في معرض. لا يزال من الممكن التعرف عليها سواء تم تصويرها تحت ضوء النهار الناعم، أو تحت الأضواء الاصطناعية الساطعة، أو حتى مع وجود ضبابية طفيفة في الحركة من كاميرا محمولة باليد. تظل النقاط الرئيسية ثابتة بما يكفي للمطابقة الدقيقة على الرغم من هذه الاختلافات.

آلية عمل خوارزمية تحويل الميزات الثابتة الحجم (SIFT)

بعد ذلك، دعنا نلقي نظرة على كيفية عمل خوارزمية SIFT. يمكن تقسيم هذه العملية إلى أربع خطوات رئيسية: اكتشاف النقاط الرئيسية، وتحديد موقع النقاط الرئيسية، وتعيين الاتجاه، ووصف النقاط الرئيسية.

الخطوة 1: الكشف عن القيم المتطرفة في فضاء المقياس

تتمثل الخطوة الأولى في العثور على النقاط الرئيسية detect وهي النقاط المميزة في الصورة، مثل الزوايا أو التغيرات الحادة في النسيج، والتي تساعد في track الجسم أو التعرف عليه.

للتأكد من إمكانية التعرف على هذه النقاط الرئيسية المحتملة بأي حجم، تقوم SIFT ببناء ما يسمى بمساحة المقياس. هذه عبارة عن مجموعة من الصور تم إنشاؤها عن طريق تمويه الصورة الأصلية تدريجيًا باستخدام مرشح Gaussian، وهي تقنية تنعيم، وتجميع النتائج في طبقات تسمى الأوكتافات. تحتوي كل أوكتاف على نفس الصورة بمستويات متزايدة من التمويه، بينما الأوكتاف التالي هو نسخة أصغر من الصورة.

عن طريق طرح صورة ضبابية من صورة أخرى، تحسب SIFT الفرق في Gaussian (DoG)، الذي يبرز المناطق التي تتغير فيها درجة السطوع بشكل حاد. يتم اختيار هذه المناطق كنقاط رئيسية مرشحة لأنها تظل ثابتة عند تكبير الصورة أو تصغيرها.

‍

الخطوة 2: تحديد موقع النقاط الرئيسية

ليست كل النقاط الرئيسية المرشحة مفيدة لأن بعضها قد يكون ضعيفًا أو غير مستقر. لتحسينها، تستخدم SIFT طريقة رياضية تسمى توسيع تايلور (Taylor Series Expansion)، مما يساعد على تقدير الموقع الدقيق للنقطة الرئيسية بدقة أكبر.

خلال هذه الخطوة، تتم إزالة النقاط غير الموثوقة. يتم تجاهل النقاط الرئيسية ذات التباين المنخفض، والتي تندمج في محيطها، وكذلك تلك التي تقع مباشرة على الحواف، لأنها يمكن أن تتحول بسهولة شديدة. تترك خطوة التصفية هذه وراءها فقط النقاط الرئيسية الأكثر استقرارًا وتميزًا.

الخطوة 3: تعيين الاتجاه

بمجرد تحديد النقاط الرئيسية المستقرة، تجعلها SIFT ثابتة الدوران، مما يعني أنه لا يزال من الممكن مطابقتها حتى إذا تم تدوير الصورة جانبًا أو رأسًا على عقب. للقيام بذلك، تحلل SIFT كيفية تغير السطوع حول كل نقطة رئيسية، وهو ما يعرف بالتدرج. تُظهر التدرجات اتجاه وقوة التغيير في كثافة البكسل، وتلتقط معًا الهيكل المحلي حول النقطة.

لكل نقطة رئيسية، يأخذ SIFT في الاعتبار التدرجات داخل منطقة محيطة ويجمعها في مخطط توزيع للاتجاهات. تشير أعلى قمة في هذا المخطط التوزيعي إلى الاتجاه السائد لتغير الشدة، والذي يتم تعيينه بعد ذلك كاتجاه للنقطة الرئيسية. يتم استخدام كل من اتجاهات التدرج، التي توضح مكان تغير الشدة، ومقادير التدرج، التي تشير إلى مدى قوة هذا التغيير، لبناء هذا المخطط التوزيعي.

إذا كانت هناك قمم أخرى قريبة من نفس القوة، فإن SIFT يعين اتجاهات متعددة لنفس النقطة الرئيسية. يمنع هذا فقدان الميزات المهمة عندما تظهر الكائنات بزوايا غير عادية. من خلال محاذاة كل نقطة رئيسية مع اتجاهها، تضمن SIFT بقاء الواصفات التي تم إنشاؤها في الخطوة التالية متسقة. 

بمعنى آخر، حتى إذا تم تدوير صورتين لنفس الكائن بشكل مختلف، فستظل النقاط الرئيسية المحاذية للاتجاه متطابقة بشكل صحيح. هذه الخطوة هي التي تمنح SIFT قدرتها القوية على التعامل مع الدوران وتجعلها أكثر قوة بكثير من طرق الكشف عن الميزات السابقة.

الخطوة 4: واصف النقطة الرئيسية

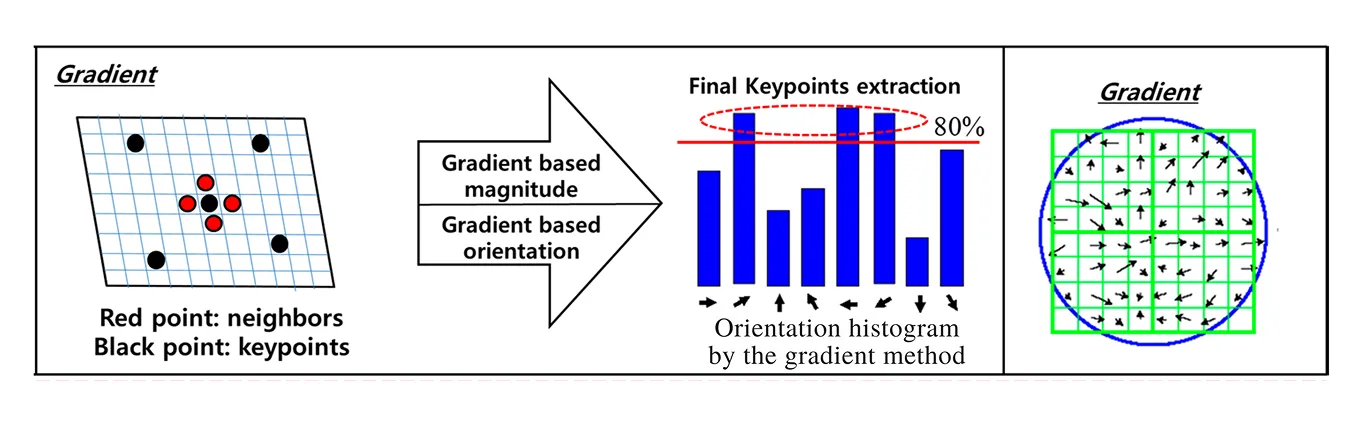
الخطوة الأخيرة في SIFT هي إنشاء وصف لكل نقطة رئيسية بحيث يمكن التعرف عليها في الصور الأخرى. 

تحقق SIFT ذلك من خلال النظر إلى رقعة مربعة صغيرة حول كل نقطة رئيسية، بحجم 16 × 16 بكسل تقريبًا. تتم محاذاة هذه الرقعة أولاً مع اتجاه النقطة الرئيسية بحيث لا يؤثر الدوران عليها. ثم يتم تقسيم الرقعة إلى شبكة من المربعات الصغيرة بحجم 4 × 4.

في كل مربع صغير، يقيس SIFT كيف يتغير السطوع في اتجاهات مختلفة. يتم تخزين هذه التغييرات في شيء يسمى المدرج التكراري، وهو يشبه الرسم البياني الذي يوضح الاتجاهات الأكثر شيوعًا. يحصل كل مربع على المدرج التكراري الخاص به، وتنتج المربعات الـ 16 معًا 16 مدرجًا تكراريًا.

أخيرًا، يتم دمج هذه المدرجات التكرارية في قائمة واحدة من الأرقام، 128 رقمًا إجمالاً. تسمى هذه القائمة متجه الميزات، وهي تعمل بمثابة بصمة للإحداثية الرئيسية. نظرًا لأنها تلتقط النسيج والهيكل الفريد حول النقطة، فإن هذه البصمة تجعل من الممكن مطابقة نفس الإحداثية الرئيسية عبر صور مختلفة، حتى إذا تم تغيير حجمها أو تدويرها أو إضاءتها بشكل مختلف.

التطبيقات الرئيسية لـ SIFT في رؤية الكمبيوتر

الآن بعد أن أصبح لدينا فهم أفضل لماهية SIFT وكيفية عملها، دعنا نستكشف بعض تطبيقاتها الواقعية في الرؤية الحاسوبية.

التعرف على الكائنات واكتشافها

أحد الاستخدامات الرئيسية ل SIFT هو التعرف على الأجسام واكتشافها. يتضمن ذلك تعليم الكمبيوتر التعرف على الأجسام في الصور وتحديد موقعها، حتى عندما لا تبدو الأجسام متشابهة دائمًا. على سبيل المثال، يمكن ل SIFT detect كتاب بغض النظر عما إذا كان قريبًا من الكاميرا أو بعيدًا أو مدورًا بزاوية.

السبب في نجاح ذلك هو أن SIFT تستخرج نقاطًا رئيسية مميزة ومستقرة للغاية. عندما تقترن هذه النقاط الرئيسية بواصفات SIFT، فإنها تشكل ميزات SIFT، التي توفر طريقة موثوقة لمطابقة نفس الكائن عبر صور مختلفة. تلتقط هذه الميزات تفاصيل فريدة للكائن تظل ثابتة، مما يتيح مطابقة الميزات بشكل موثوق عبر الصور حتى عندما يتغير حجم الكائن أو موضعه أو اتجاهه.

‍

قبل أن يصبح التعلم العميق شائعًا، كانت SIFT واحدة من أكثر الطرق موثوقية لبناء أنظمة التعرف على الكائنات. وقد استخدمت على نطاق واسع في الأبحاث والتطبيقات التي تتطلب مطابقة الكائنات عبر مجموعات بيانات صور كبيرة، على الرغم من أنها غالبًا ما تتطلب موارد حسابية كبيرة.

تجميع الصور وإنشاء بانوراما

يمكن أيضًا استخدام SIFT لإنشاء صور بانورامية، وهي صور واسعة مصنوعة عن طريق تجميع عدة صور معًا. باستخدام SIFT، يتم العثور على نقاط رئيسية مميزة في الأجزاء المتداخلة من الصور المختلفة ثم مطابقتها مع بعضها البعض. تعمل هذه التطابقات بمثابة نقاط ارتكاز، وتوجه عملية التجميع حول كيفية محاذاة الصور.

بمجرد اكتمال المطابقة، يمكن استخدام خوارزميات التجميع لحساب المحاذاة الصحيحة، غالبًا باستخدام التحويلات الهندسية التي ترسم صورة واحدة على أخرى. ثم يتم دمج الصور بحيث تختفي اللحامات. النتيجة النهائية هي صورة بانورامية سلسة تبدو وكأنها صورة واسعة واحدة، على الرغم من أنها تم إنشاؤها من لقطات متعددة.

إعادة البناء ثلاثي الأبعاد والروبوتات

تطبيق آخر مثير للاهتمام لـ SIFT هو في إعادة البناء ثلاثية الأبعاد، حيث يتم دمج صور ثنائية الأبعاد متعددة مأخوذة من زوايا مختلفة لبناء نموذج ثلاثي الأبعاد. يعمل SIFT من خلال إيجاد ومطابقة نفس النقاط عبر هذه الصور. 

بمجرد إجراء المطابقات، يمكن تقدير المواضع ثلاثية الأبعاد لتلك النقاط باستخدام التثليث، وهي طريقة تحسب العمق من وجهات نظر مختلفة. هذه العملية هي جزء من الهيكل من الحركة (SfM)، وهي تقنية تستخدم صورًا متداخلة متعددة لتقدير الشكل ثلاثي الأبعاد لمشهد ما جنبًا إلى جنب مع مواضع الكاميرات التي التقطت الصور.

النتيجة عادة ما تكون سحابة نقاط ثلاثية الأبعاد، وهي عبارة عن مجموعة من النقاط في الفضاء تحدد الكائن أو البيئة. كانت SIFT واحدة من الأدوات الأولى التي جعلت الهيكل من الحركة عمليًا. في حين أن التقنيات الأحدث أسرع وأكثر شيوعًا اليوم، إلا أن SIFT لا تزال تُستخدم عندما تكون الدقة أكثر أهمية من السرعة.

تم استخدام SIFT أيضًا في الروبوتات، وخاصة في SLAM البصري (التوطين ورسم الخرائط المتزامنين). يسمح SLAM للروبوت بمعرفة مكانه أثناء بناء خريطة لمحيطه في نفس الوقت. 

تعمل النقاط الرئيسية في SIFT كمعالم موثوقة يمكن للروبوت التعرف عليها عبر الإطارات، حتى عندما تتغير الإضاءة أو الزوايا. من خلال تتبع هذه المعالم، يمكن للروبوت تقدير موضعه وتحديث خريطته أثناء التنقل. على الرغم من أن كاشفات الميزات الأسرع تستخدم غالبًا في الروبوتات اليوم، إلا أن SIFT لعبت دورًا مهمًا في أنظمة SLAM المبكرة ولا تزال أساسية في الحالات التي تكون فيها المتانة أكثر أهمية من السرعة.

مزايا واعتبارات SIFT

في حين أن خوارزمية SIFT قد استخدمت على نطاق واسع في الرؤية الحاسوبية وتشتهر بكونها طريقة موثوقة، إلا أنها تأتي أيضًا مع بعض المقايضات. لهذا السبب من المهم موازنة إيجابياتها وسلبياتها قبل تحديد ما إذا كانت مناسبة تمامًا للمشروع. بعد ذلك، دعنا نسير في نقاط القوة والقيود الرئيسية.

المزايا الأساسية لـ SIFT

فيما يلي بعض إيجابيات استخدام خوارزمية SIFT:

• مقياس وثبات الدوران: يوفر SIFT نقاطًا رئيسية ثابتة المقياس تظل مستقرة نسبيًا عندما تظهر الكائنات بأحجام أو اتجاهات مختلفة، وهو ما يمثل خطوة كبيرة إلى الأمام مقارنةً بكاشفات الميزات السابقة.‍
• مرونة معتدلة للتغيرات في الإضاءة ووجهة النظر: يمكن لـ SIFT التعامل مع التغيرات في السطوع أو التباين أو التحولات الصغيرة في وجهة النظر، على الرغم من أنه أقل موثوقية في الظروف الأكثر قسوة.‍
• القدرة على العمل في مشاهد مزدحمة أو مخفية جزئيًا: نظرًا لأن SIFT يكتشف العديد من النقاط الرئيسية المحلية، فإنه غالبًا ما يظل قادرًا على تحديد الكائن حتى لو كان جزء منه مغطى أو كانت الخلفية معقدة.

اعتبارات الأداء وبدائله

فيما يلي بعض عيوب استخدام خوارزمية SIFT:

• مكلفة حسابيًا: إن عملية SIFT متعددة الخطوات والموصِّفات التفصيلية تجعلها أبطأ وأكثر استهلاكًا للموارد من كاشفات الميزات الحديثة. ولتحسين ذلك، طور الباحثون خوارزمية SURF (الميزات القوية المتسارعة)، التي تستخدم حسابات أسرع للعثور على الميزات ووصفها. SURF أقل دقة من SIFT في بعض الحالات، ولكنه يعمل بشكل أسرع بكثير، مما يجعله أكثر عملية للمهام الحساسة للوقت.‍
• غير مثالي للاستخدام في الوقت الفعلي: نظرًا لتكلفته الحسابية، يكافح SIFT عندما يتعلق الأمر بالتطبيقات التي تكون فيها السرعة بالغة الأهمية، مثل التتبع في الوقت الفعلي أو الروبوتات المتنقلة.‍
• تنوع محدود: على الرغم من قوة SIFT في العديد من الحالات، إلا أنها أقل فعالية في تغييرات الإضاءة الشديدة أو تحولات وجهة النظر الكبيرة أو المشاهد الديناميكية للغاية حيث تعمل الخوارزميات الأحدث أو طرق التعلم الآلي بشكل أفضل.

‍

أثناء استكشاف إيجابيات وسلبيات SIFT، قد تلاحظ أن العديد من قيودها مهدت الطريق لتقنيات أكثر تقدمًا. على وجه التحديد، ظهرت الشبكات العصبية التلافيفية (CNNs) كبديل قوي. 

الشبكة العصبية الالتفافية (CNN) هي نوع من نموذج التعلم العميق مستوحى من طريقة عمل نظام الرؤية البشري. يقوم بمعالجة الصورة في طبقات، بدءًا من الأنماط البسيطة مثل الحواف والتركيبات، والتراكم تدريجيًا إلى الأشكال والكائنات الأكثر تعقيدًا. على عكس قواعد الميزات المصممة يدويًا في SIFT، تتعلم الشبكات العصبية الالتفافية تمثيلات الميزات مباشرة من البيانات. 

يعني هذا التعلم القائم على البيانات أن CNNs يمكن أن تتفوق على SIFT في مطابقة الواصفات ومهام التصنيف. تعتبر CNNs أيضًا أكثر تعبيرًا وقوة، وتتكيف بشكل أفضل مع تقلب وتعقيد البيانات المرئية. 

على سبيل المثال، حققت النماذج المستندة إلى شبكة CNN نتائج مذهلة على ImageNetوهي مجموعة بيانات معيارية ضخمة تحتوي على ملايين الصور المصنفة عبر آلاف الفئات. صُممت ImageNet لاختبار مدى قدرة الخوارزميات على التعرف على الأشياء classify وهي قادرة على تسليط الضوء على الفجوة بين الأساليب القديمة القائمة على السمات والتعلم العميق. 

تفوقت الشبكات العصبونية الالتفافية (CNN) بسرعة على SIFT من خلال تعلم تمثيلات أكثر ثراءً ومرونة، مما سمح لها بالتعرف على الكائنات في ظل الإضاءة المتغيرة، ومن وجهات نظر مختلفة، وحتى عندما تكون مخفية جزئيًا، وهي سيناريوهات غالبًا ما تعاني فيها SIFT.

النقاط الرئيسية

تحتل خوارزمية تحويل الملامح الثابتة بالمقياس مكانة مهمة في تاريخ الرؤية الحاسوبية. فقد وفرت طريقة موثوقة detect الميزات حتى في البيئات المتغيرة وأثرت على العديد من الطرق المستخدمة اليوم. 

في حين أن التقنيات الأحدث أسرع وأكثر كفاءة، إلا أن SIFT وضعت الأساس لها. تعرض SIFT من أين بدأ التقدم الحالي في الرؤية الحاسوبية وتسلط الضوء على المدى الذي وصلت إليه أنظمة الذكاء الاصطناعي المتطورة.

انضم إلى مجتمعنا العالمي وتحقق من مستودع GitHub الخاص بنا لمعرفة المزيد حول رؤية الحاسوب. استكشف صفحات الحلول الخاصة بنا لاكتشاف ابتكارات مثل الذكاء الاصطناعي في الزراعة ورؤية الحاسوب في مجال البيع بالتجزئة. تحقق من خيارات الترخيص لدينا وابدأ في بناء نموذج رؤية الحاسوب الخاص بك.