Learn how quantum optimization is redefining AI and deep learning. Explore how quantum algorithms, qubits, and hybrid computing drive smarter, faster models.

Learn how quantum optimization is redefining AI and deep learning. Explore how quantum algorithms, qubits, and hybrid computing drive smarter, faster models.

Most cutting-edge AI systems, from a self-driving car to a stock prediction model, are constantly making trade-offs as they adjust, refine, and learn from experience. Behind these decisions lies one of the most important processes in AI: optimization.
For instance, an AI model trained to recognize traffic signs or predict house prices learns from examples. As it trains, it continually improves how it learns. Each step adjusts millions of parameters, fine-tuning weights and biases to reduce prediction errors and improve accuracy.
You can think of this process as a large-scale optimization problem. The goal is to find the best combination of parameters that delivers accurate results without overfitting or wasting computational resources.
In fact, optimization is a key part of artificial intelligence. Whether an AI model is identifying an image or forecasting a price, it must search for the most effective solution among countless possibilities. But as models and datasets grow, this search becomes increasingly complex and computationally expensive.
Quantum optimization is an emerging approach that could help solve this challenge. It’s based on quantum computing, which uses the principles of quantum mechanics to process information in new ways.
Instead of bits that can only be 0 or 1, quantum computers use qubits that can exist in multiple states at once. This lets them explore many possible solutions in parallel, solving complex optimization problems more efficiently than classical methods in some cases.
However, quantum parallelism is not the same as running many classical processors at the same time. It is a probabilistic process that depends on quantum interference to produce useful results.
Simply put, that means quantum computers don’t test every possibility at once. Instead, they use interference, where certain possibilities reinforce each other and others cancel out, to increase the chances of finding the right answer.
In this article, we’ll explore how quantum optimization works, why it matters, and what it could mean for the future of intelligent computing. Let’s get started!
Quantum optimization is a growing field within quantum computing that focuses on solving complex optimization problems using the unique properties of quantum mechanics. It builds on decades of computer science and physics research, combining them to tackle challenges that traditional computing struggles with.
The idea of using quantum systems for optimization first emerged in the late 1990s when researchers began exploring how quantum principles like superposition (simultaneous states) and entanglement (linked qubits) could be applied to problem-solving.
Over time, this evolved into quantum optimization, where researchers developed algorithms that use quantum effects to efficiently search for optimal solutions across large and complex problem spaces.
At its core, quantum optimization is built on three key components: quantum algorithms, qubits, and quantum circuits. Quantum algorithms provide the logic that enables efficient exploration of large sets of possible solutions.
These algorithms operate on qubits, the fundamental units of quantum information, which differ from classical bits (the binary units of data in traditional computers that can hold a value of either 0 or 1) because they can exist in a state of superposition, representing both 0 and 1 at the same time.
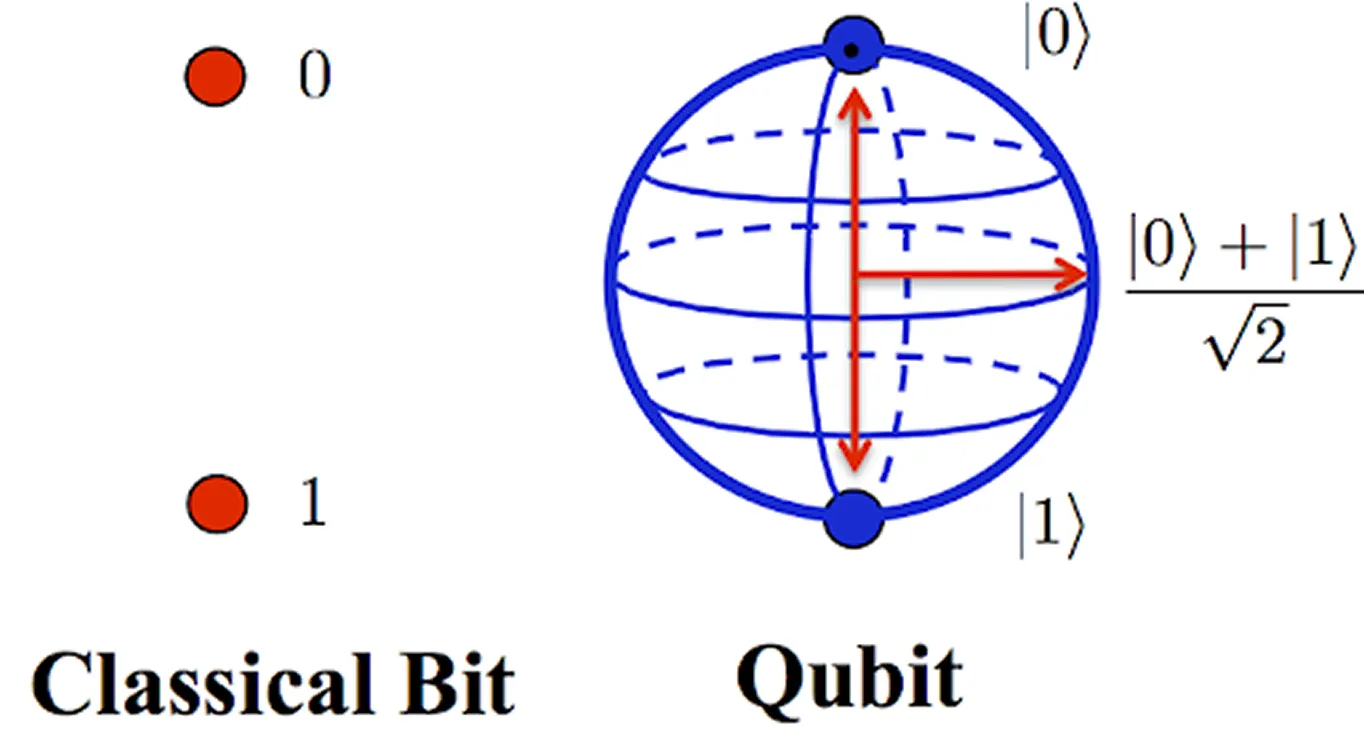
This unique property enables quantum systems to evaluate multiple possibilities simultaneously, significantly expanding their computational potential. Meanwhile, quantum circuits connect qubits through sequences of quantum gates, which control how information flows and interacts to guide the system toward a near-optimal solution gradually.
Here are a few key differences between classical and quantum optimization approaches:

Next, let’s walk through how quantum optimization actually works. It all starts with defining a real-world problem and translating it into a form a quantum computer can process.
Here’s an overview of the main steps involved in quantum optimization:
Thanks to recent advances in quantum computing, researchers have developed a range of quantum optimization algorithms that aim to solve complex problems more efficiently. These approaches are shaping the future of the field. Let’s take a look at some of the main ones.
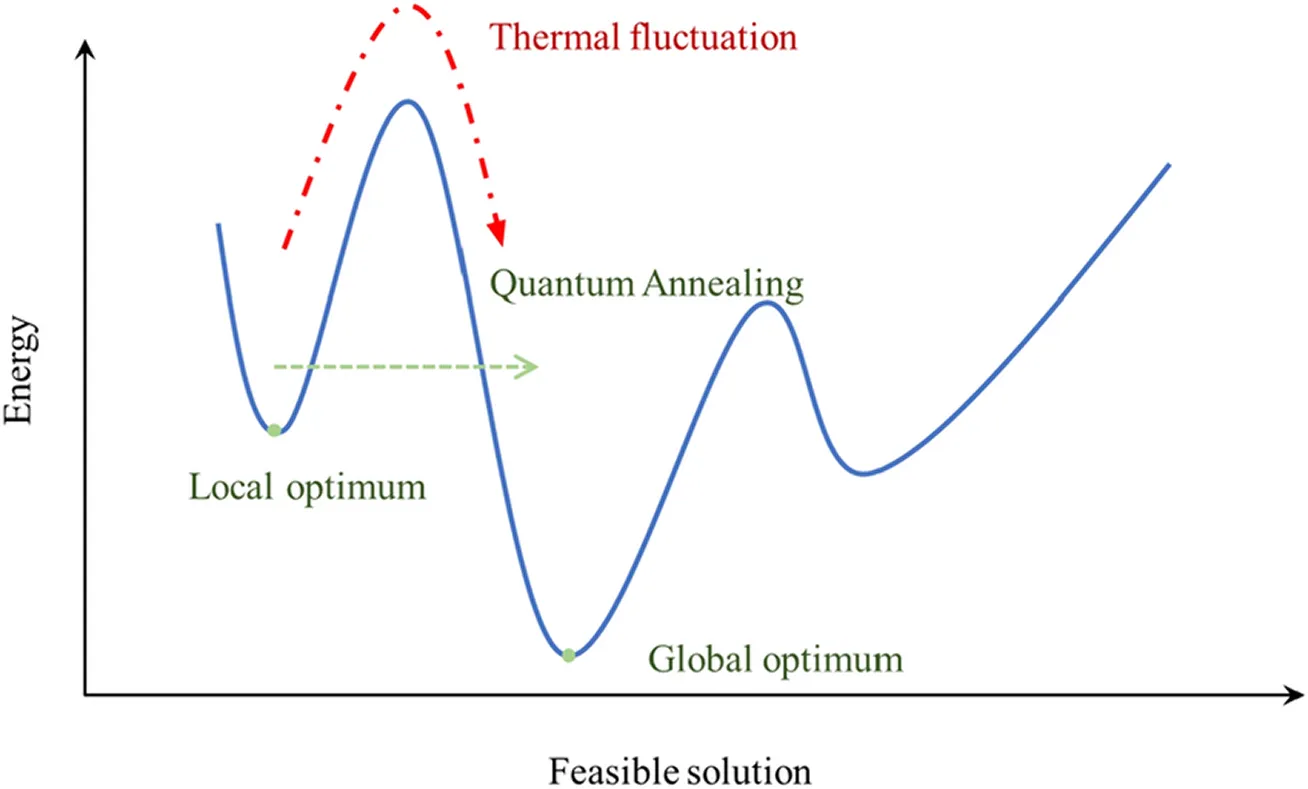
Quantum annealing is a technique used to solve optimization problems that involve finding the best arrangement or combination from many possibilities. These are called combinatorial optimization problems, such as scheduling deliveries, routing vehicles, or grouping similar data points.
The method is inspired by a physical process known as annealing, where a material is slowly cooled to reach a stable, low-energy state. In a similar way, quantum annealing gradually guides a quantum system toward its lowest energy state, which represents the best possible solution to the problem.
This process, based on the principles of adiabatic quantum computation, allows the system to explore many potential solutions and settle into one that is close to optimal. Because results are probabilistic, the process is usually repeated multiple times, with classical computing often used afterward to refine the answers.
Quantum annealing shows potential for solving real-world optimization problems in areas such as logistics, clustering, and resource allocation. However, researchers are still exploring when and how it might perform better than traditional methods.
The Quantum Approximate Optimization Algorithm (QAOA) also handles combinatorial optimization problems, but in a different way from quantum annealing. Instead of gradually evolving toward the lowest energy state, QAOA alternates between two energy functions, called Hamiltonians.
One represents the problem’s objective and constraints, while the other helps the system explore new configurations. By switching between these stages, the algorithm steadily moves toward a near-optimal solution.
QAOA runs on hybrid quantum and classical systems, where the quantum computer generates possible solutions and a classical computer adjusts parameters after each run. This approach makes QAOA a flexible tool for many optimization tasks, including scheduling, routing, and graph problems such as MaxCut (finding the best way to divide a network into two parts) and vertex cover (selecting the smallest set of nodes that connect to every edge in a network). While research is still underway, QAOA is widely seen as a promising step toward combining classical and quantum optimization.
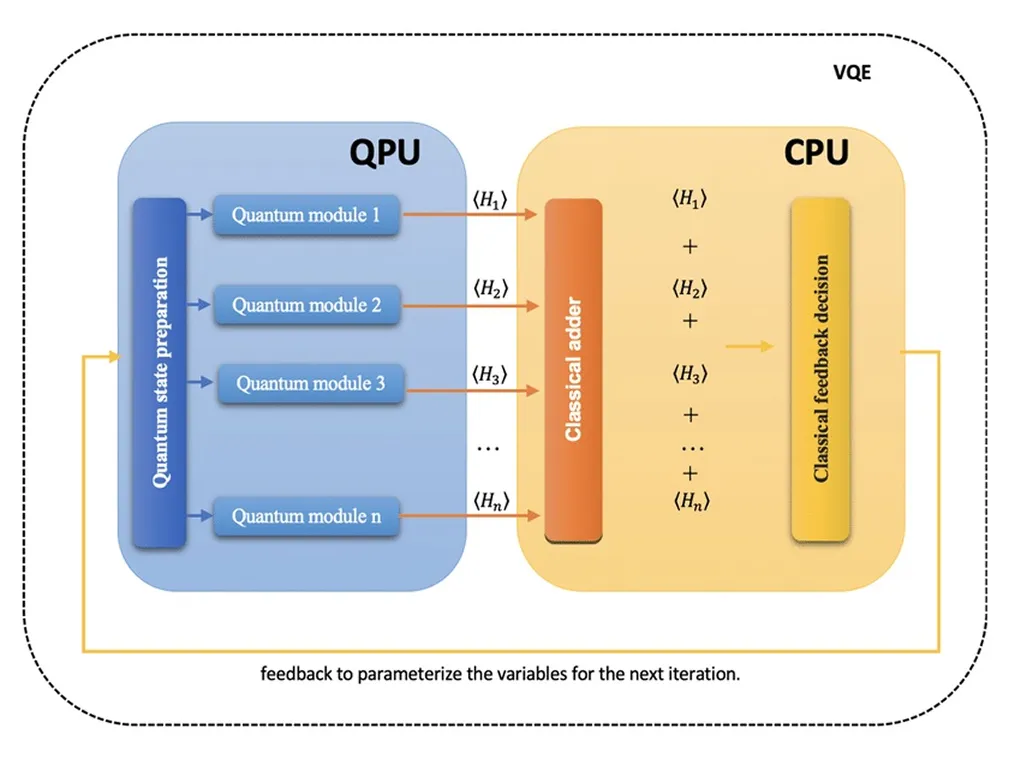
Another important algorithm is the Variational Quantum Eigensolver (VQE). Unlike QAOA and quantum annealing, which handle combinatorial optimization problems involving discrete choices, VQE focuses on continuous optimization, where variables can take on a range of values instead of fixed options.
It is mainly used to estimate the ground state, or the lowest possible energy, of a quantum system. This makes it especially useful for studying molecular and material behavior in physics and chemistry.
VQE also uses a hybrid approach that combines quantum and classical computing. The quantum computer prepares and tests possible states, while the classical computer analyzes the results and adjusts parameters to improve accuracy.
Because it requires fewer qubits and simpler circuits, VQE performs well on current NISQ (Noisy Intermediate Scale Quantum) devices. These are today’s generation of quantum computers that have a limited number of qubits and are affected by noise, but are still powerful enough for research and early practical experiments.
VQE has become an essential tool in quantum chemistry, materials science, and process optimization. It helps researchers model molecules, study reactions, and find stable configurations.
Semidefinite programming (SDP) is a mathematical method used to solve optimization problems that include linear relationships between variables. It is often applied when the goal is to find the best possible outcome while keeping certain conditions within a valid range.
Quantum SDP algorithms aim to make these calculations faster, especially when the data involves many variables or complex, high-dimensional spaces. They use principles of quantum computing to analyze several possibilities at once, which can make solving large-scale problems more efficient.
These algorithms are being explored in fields such as machine learning, signal processing, and control systems, where they could help models recognize patterns, improve predictions, or manage complex systems. Although research is still ongoing, quantum SDP shows promise for speeding up advanced optimization tasks that are difficult for classical computers.
While quantum optimization is an active area of research, it is also beginning to find practical applications in fields such as artificial intelligence and machine learning. Researchers are exploring how quantum methods can help solve complex problems more efficiently.
Next, we’ll take a closer look at some of the emerging examples and use cases that highlight its potential in real-world scenarios.
Quantum optimization is being explored to improve how machine learning models are tuned, particularly with respect to hyperparameter optimization and feature selection. Recent advances in neutral atom processors are also expanding the scope of quantum optimization experiments in AI and machine learning.
These processors use individual atoms held in place by lasers to act as qubits. This allows researchers to build scalable and stable quantum systems for testing complex algorithms.
Leading technology companies are already experimenting with these ideas. For example, Google’s research team recently demonstrated a generative quantum advantage, where a 68-qubit processor learned to generate complex distributions, hinting at applications in training generative models.
Similarly, NVIDIA is building bridges between quantum and AI by integrating quantum research into its supercomputing and GPU ecosystem. For example, it launched an Accelerated Quantum Research Center (NVAQC) to combine quantum hardware with AI systems.
In addition to this, AWS has developed a hybrid quantum and classical workflow on Amazon Braket that uses quantum circuits together with classical optimization to fine-tune parameters for image classification tasks.
One of the most practical areas for quantum optimization is logistics and scheduling. These tasks include route planning, vehicle assignment, and resource distribution.
A good example is energy grid scheduling, where operators must balance electricity supply and demand in real time while reducing cost and maintaining reliability. Researchers have used quantum optimization to represent this scheduling challenge as an energy landscape or a Hamiltonian.
Here, the goal is to find the lowest energy state, which represents the most efficient configuration. For example, D Wave’s quantum solvers have been tested for such problems and have shown faster and more flexible results compared with traditional optimization methods.
Similar ideas are now being studied in areas like portfolio management and supply chain planning. As hardware improves, these approaches may change how AI systems plan and make decisions under real-world constraints.
Quantum optimization is also gaining attention in areas where understanding complex molecular interactions and energy landscapes is critical. For example, in drug discovery and materials science, finding the most stable molecular structures or configurations is an optimization challenge.
Hybrid quantum algorithms, such as the VQE, are being used to speed up processes like protein structure prediction and molecular conformation search. Researchers are also exploring ways to combine quantum computing and artificial intelligence to improve how models learn and extract features from data.
As quantum hardware continues to advance, these combined approaches could lead to major breakthroughs in chemistry, biology, and materials research, enabling faster discovery and more accurate simulations at the molecular level.
Here are some of the advantages of using quantum optimization:
Even though quantum research is advancing quickly, there are still certain challenges that prevent large-scale adoption. Here are some of the key limitations to consider:
Quantum optimization is reshaping how we think about problem-solving in artificial intelligence, science, and industry. By combining the power of quantum computing with classical methods, researchers are finding new ways to handle complexity and accelerate discovery. As hardware improves and algorithms mature, quantum optimization could become a key driver of the next generation of intelligent technologies.
Check out our GitHub repository to discover more about AI. Join our active community and discover innovations in sectors like AI in the retail industry and Vision AI in manufacturing. To get started with computer vision today, check out our licensing options.