Confusion Matrix

A confusion matrix is a comprehensive performance measurement tool used in machine learning (ML) to evaluate the accuracy of a classification model. Unlike a simple accuracy score, which only tells you the percentage of correct predictions, a confusion matrix provides a granular breakdown of how the model categorizes each class. It visualizes the discrepancy between the predicted labels and the actual ground truth, allowing developers to pinpoint exactly where a model is "confused" or making systematic errors. This level of detail is vital for refining complex computer vision (CV) systems, such as those built with Ultralytics YOLO11.

Core Components of the Matrix

A confusion matrix breaks down the predictions of a classifier into four distinct categories, typically arranged in a grid layout. These components help in identifying whether a model suffers from specific types of error, such as "false alarms" or "missed targets":

• True Positives (TP): The model correctly predicts the positive class. For instance, in object detection, the model successfully identifies a pedestrian crossing the street.
• True Negatives (TN): The model correctly predicts the negative class. In a defect detection system for AI in manufacturing, this occurs when the model correctly identifies a functional part as non-defective.
• False Positives (FP): The model incorrectly predicts the positive class. This is often called a Type I error. An example is a security camera flagging a swaying tree branch as an intruder.
• False Negatives (FN): The model incorrectly predicts the negative class. This is known as a Type II error. This would happen if a medical diagnostic tool failed to detect a tumor that is actually present.

Significance in Model Evaluation

While broad metrics are useful for high-level overviews, the confusion matrix is essential when dealing with imbalanced datasets. If a dataset contains 95 cats and 5 dogs, a model that simply guesses "cat" every time achieves 95% accuracy but is useless for finding dogs. The confusion matrix would reveal this failure immediately by showing zero True Positives for the "dog" class.

This breakdown serves as the foundation for calculating other critical performance metrics. By analyzing the matrix, engineers can derive:

• Precision: The accuracy of positive predictions (TP / (TP + FP)).
• Recall (Sensitivity): The ability to capture all actual positive cases (TP / (TP + FN)).
• F1-Score: A harmonic mean of precision and recall, offering a balanced view of the model's robustness.

Real-World Applications

The importance of the confusion matrix varies depending on the specific application and the "cost" of different errors.

• Medical Diagnostics: In AI in healthcare, the cost of a False Negative is extremely high. If a model is designed to detect pneumonia from X-rays, missing a positive case (FN) could delay life-saving treatment. Therefore, developers analyze the confusion matrix to maximize Recall, ensuring even subtle signs of disease are flagged for human review. You can read more about evaluation in medical imaging to understand these stakes.
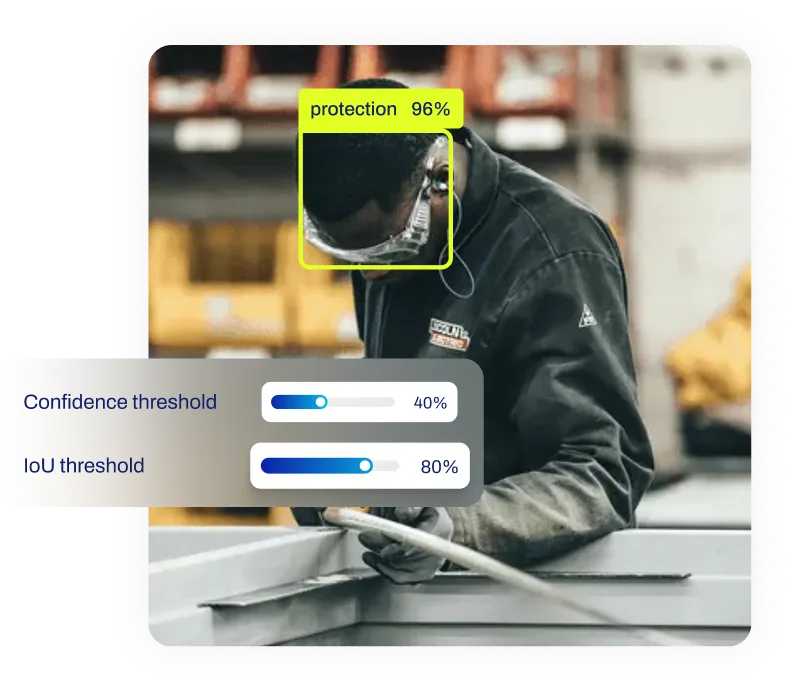
• Fraud Detection: In financial systems, a False Positive (flagging a legitimate transaction as fraud) can annoy customers and block access to funds. However, a False Negative (allowing actual fraud) causes direct financial loss. By using a confusion matrix, data scientists can tune the confidence threshold to find the optimal trade-off, balancing security with user experience.
• Autonomous Vehicles: For self-driving cars, distinguishing between a stationary object and a moving pedestrian is critical. A confusion matrix helps engineers understand if the system frequently confuses specific classes, such as mistaking a lamppost for a person, allowing for targeted data augmentation to correct the behavior.

Analyzing Results with Code

The ultralytics library automatically computes and saves confusion matrices during the validation process. This allows users to visualize performance across all classes in their dataset.

from ultralytics import YOLO

# Load the YOLO11 model
model = YOLO("yolo11n.pt")

# Validate the model on a dataset like COCO8
# This generates the confusion matrix in the 'runs/detect/val' directory
results = model.val(data="coco8.yaml")

# You can also programmatically access the matrix data
print(results.confusion_matrix.matrix)

Comparison to Related Terms

It is important to distinguish the confusion matrix from derived metrics. While Accuracy, Precision, and Recall are single-number summaries, the Confusion Matrix is the raw data source from which those numbers are calculated. It provides the "whole picture" rather than a snapshot. Additionally, in object detection, the matrix often interacts with Intersection over Union (IoU) thresholds to determine what counts as a True Positive, adding another layer of depth to the evaluation in computer vision tasks.