Markov Decision Process (MDP)

A Markov Decision Process (MDP) is a mathematical framework used to model decision-making in situations where outcomes are partly random and partly under the control of a decision-maker. It serves as the theoretical foundation for Reinforcement Learning (RL), providing a formal way to describe an environment in which an AI agent operates. By structuring problems into states, actions, and rewards, MDPs enable intelligent systems to calculate the best strategy, known as a policy, to maximize specific goals over time. This framework is essential for developing advanced technologies, from automated trading systems to autonomous vehicles.

Core Components of an MDP

An MDP characterizes the interaction between an agent and its environment using five distinct elements. These components allow researchers to define complex machine learning (ML) problems in a solvable format:

• States (S): The set of all possible situations the agent can occupy. In a chess game, a state represents the current configuration of pieces on the board.
• Actions (A): The set of all possible moves or decisions the agent can make from a given state.
• Transition Probability: The likelihood of moving from one state to another after performing a specific action. This component models the uncertainty in the environment, often described as a stochastic process.
• Reward Function: A feedback signal that quantifies the immediate benefit of taking a specific action in a specific state. The agent uses this signal to evaluate its performance.
• Policy ($\pi$): A strategy or rulebook that defines the agent's behavior. The goal of solving an MDP is to find an "optimal policy" that maximizes the total expected reward over the long run.

The central assumption of this framework is the Markov property, which states that the future evolution of the process depends only on the current state and not on the sequence of events that preceded it. This simplifies the computational requirements for making optimal decisions.

Real-World Applications

MDPs are widely used across various industries to solve sequential decision-making problems where planning and adaptability are crucial.

• Robotics: Robots often operate in dynamic environments where sensors provide noisy data. An MDP allows a robot to plan its path by treating its location as the state and its movements as actions. Vision systems, powered by object detection models like YOLO11, help the robot perceive the state of the world—such as the presence of obstacles—allowing it to navigate safely and efficiently.
• Inventory Management: In supply chain logistics, businesses use MDPs to optimize stock levels. Here, the state is the current inventory, and the actions involve deciding how much product to reorder. The reward function balances the profit from sales against storage costs and lost revenue from stockouts, a critical application in AI for retail.
• Healthcare Treatment Planning: MDPs assist in designing personalized treatment plans for patients with chronic conditions. By modeling patient health as a series of states, doctors can determine the optimal sequence of treatments to maximize long-term health outcomes, leveraging insights from medical image analysis.

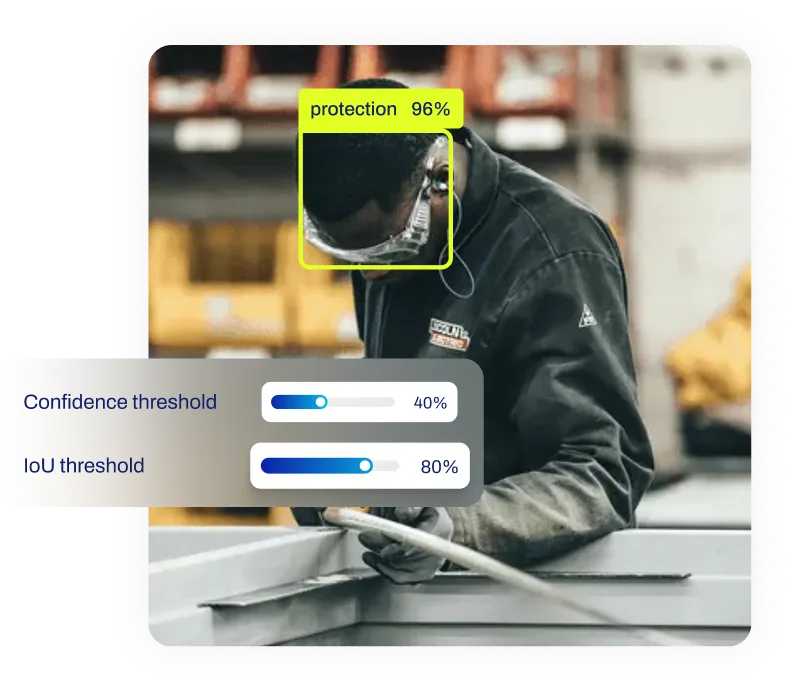
Perception as State Input

In modern AI applications, the "state" of an MDP is often derived from high-dimensional data, such as video feeds. A computer vision (CV) model processes visual input to create a structured state representation that the decision-making algorithm can understand.

The following Python code demonstrates how to use a pretrained YOLO11 model to extract state information (object coordinates) from an image. This data can serve as the input state for an MDP-based agent.

from ultralytics import YOLO

# Load a pretrained YOLO11 model to act as the perception system
model = YOLO("yolo11n.pt")

# Perform inference on an image to observe the current 'state'
# In a real MDP, this would be a frame from the agent's environment
results = model("https://ultralytics.com/images/bus.jpg")

# Extract bounding box coordinates to represent the state
state_vector = results[0].boxes.xywh
print(f"Current State Observation: {state_vector}")

Distinguishing Related Concepts

It is helpful to differentiate MDPs from other related terms in the artificial intelligence (AI) landscape:

• Reinforcement Learning (RL): While often used interchangeably, the distinction is important. An MDP is the framework or problem statement, while RL is the method used to solve it when the transition probabilities and reward functions are not initially known. Agents learn the optimal policy through trial and error, as described in foundational texts by Sutton and Barto.
• Hidden Markov Model (HMM): An HMM is used when the true state of the system is not fully observable and must be inferred from probabilistic outputs. In contrast, a standard MDP assumes the agent has full visibility of the current state.
• Deep Reinforcement Learning (DRL): DRL combines MDPs with deep learning (DL). Traditional MDP solvers struggle with massive state spaces (like the number of possible pixel combinations in a video game). DRL uses neural networks to approximate the value of states, enabling solutions for complex environments simulated in tools like Gymnasium.